오늘의 진도: 2.4. Some positive definite graphs
오늘의 요약:
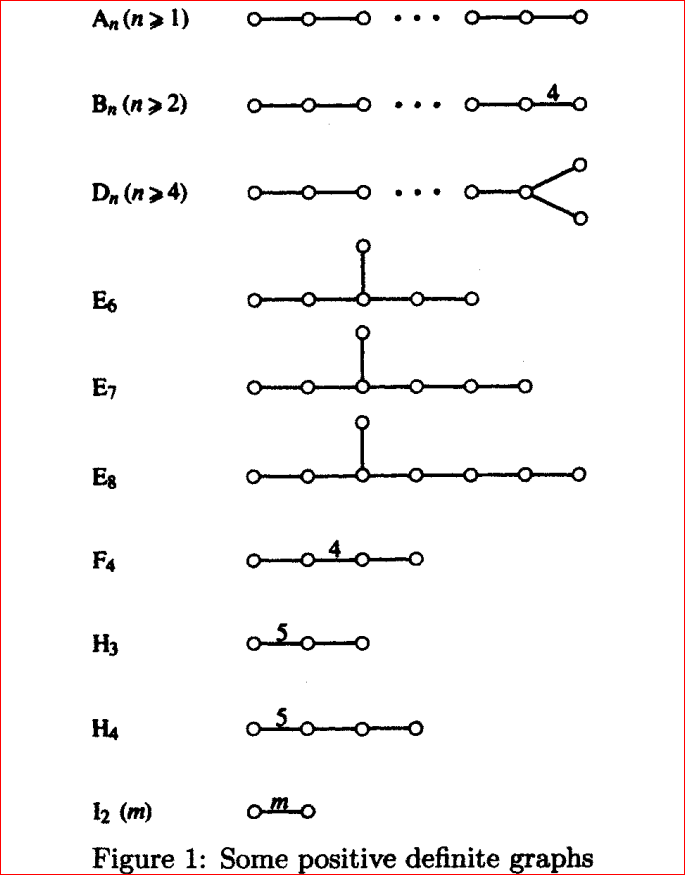
1. Figure 1의 그래프들은 positive definite graph들의 예이다...(*)
2. 두 가지 질문이 남는다:
(1) 이게 다인가?
(2) Figure 1의 positive definite graph가 실제로 어떤 유한반사군의 simple system으로부터 유도되는가?
이 질문들에 대답하는 것이 2단원의 나머지 부분이지만, 시간 관계상 내일부터는 4단원을 읽어볼 생각이다.
(*)의 증명.
어떤 행렬이 양정부호이기 위한 필요충분조건은, 모든 주대각 소행렬 (principal minor)의 행렬식이 0보다 큰 것이다.
일단, $I_{2}(m)$의 경우 행렬을 직접 표현할 수 있다:
$$A = \begin{pmatrix} 1 & -\cos(\frac{\pi}{m}) \\ -\cos(\frac{\pi}{m}) & 1 \end{pmatrix}$$
따라서 $det(A) = 1 - \cos^{2}(\frac{\pi}{m}) > 0$이고, A는 양정부호이다.
다른 경우들을 생각해 보자. $-\cos(\frac{\pi}{3}) = - \frac{1}{2}$이므로 편의상 2A의 행렬식을 구한다고 생각하자.
점의 순서를 적당히 재배열함으로써, n번째 (즉 마지막) 점이 n-1번째의 점과만 연결되고, 연결된 선분에 대응되는 숫자가 3이거나 4가 되도록 만들 수 있다.
이제 2A의 $i \times i$ 주대각 소행렬의 행렬식을 $d_{i}$라 표기하면,
$$det(2A) = 2d_{n-1} - c d_{n-2}$$이고,
대응되는 숫자가 3이면 c = 1, 숫자가 4면 c = 2가 된다. (이는, 마지막 행의 n-1번째와 n번째 성분을 제외하면 모두 0이기 때문에 가능하다).
이제 각 행렬에 대해서 $(n-1) \times (n-1)$ 소행렬을 고려하는 것은, 각 그래프에 대해서 다른 한 점과만 연결되어 있는 점과 선분을 제외한 부분 그래프에 대응하는 행렬을 고려하는 것과 같다.
그런데 Figure 1의 그래프들에서 가장자리에 있는 점과 선분을 제외하더라도, 여전히 Figure 1에 있는 그래프가 되도록 만들 수 있다. 이를 이용하여 계산을 진행하면 증명이 끝난다.
예컨대, $E_{8}$의 가장자리 점과 선분을 제외한 후 나올 수 있는 그래프는 $A_{8}$ 또는 $E_{7}$이 있고, $(n-2) \times (n-2)$의 경우는 $E_{6}, A_{7}$이 있다.
계산을 하면 (직접 해보지는 않았다) 다음의 표가 나온다고 한다:

따라서 위의 그래프들은 모두 양의 정부호이다.
'수학 (2023-S) > Reflection groups and Coxeter groups' 카테고리의 다른 글
| Reflection groups and Coxeter groups - 08.11 (0) | 2023.08.11 |
|---|---|
| Reflection groups and Coxeter groups - 08.02 (0) | 2023.08.02 |
| Reflection groups and Coxeter groups - 07.25 (0) | 2023.07.25 |
| Reflection groups and Coxeter groups - 07.24 (0) | 2023.07.24 |
| Reflection groups and Coxeter groups - 07.23 (0) | 2023.07.23 |