오늘은 학교에서 무료 나눔을 해주었던 계승혁 교수님의 <군과 조화해석>을 펼쳐보았다. 당연히 내가 다 이해할 수 있는 내용이라고 생각하지는 않았지만 컨볼루션 연산자가 군의 표현론과 어떻게 관련이 된다는 주장이 흥미로워서 더 읽어보려고 했었다.
그런데 처음부터 위상군 내용이 나왔다. 위상군을 하지는 않았었지만 Munrkes에 부록으로 등장하는 것은 알고 있기에, 위상군 내용을 조금 복습해보고, 연습문제를 조금 풀어보고자 한다.
정의. (위상군)
G가 군이라 하자. 이제 G에 $\mathcal{T}_{1}$ 공리를 만족하는 위상 $\mathcal{T}$가 주어져 있고, 두 연산
$$f: G \times G \to G, f(s,t):= st \\ g: G \to G, g(s) := s^{-1}$$
가 연속이라 하자. 이러면 G를 위상군이라 한다.
<연습문제>
1. H가 군이고, $\mathcal{T}_{1}$ 공리를 만족하는 위상공간이라 하자.
$$h: H \times H \to H, h(x,y):= xy^{-1}$$
이 연속인 것과 H가 위상군인 것이 동치임을 보이시오.
풀이.
함수 $g: H \to H, g(y):= y^{-1}$를 생각해 보면, $g(y) = h(e,y)$임을 알 수 있다. 따라서 $y^{-1} \in U$가 G의 열린집합이라 하면, $(e,y) \in h^{-1}(y^{-1})$이고, 어떤 기저집합 $V \times W \subset H \times H$가 존재하여 $h(V \times W) \subset U$가 성립한다. 다시, 이는 $g(W) \subset U$임을 의미하고, W는 G의 열린집합이므로 $g$는 연속이다.
이제, $\tilde{g}: G \times G \to G \times G, \tilde{g}(x,y) := (x, y^{-1})$는 연속이다. 또한, $h \circ \tilde{g}$는 앞서 정의한 곱 함수인데, 연속함수의 합성이므로 연속이다.
4. $\alpha \in G$라 하자. 다음의 사상들
$$f_{\alpha}: G \to G, f_{\alpha}(x) = \alpha x \\ g_{\alpha}: G \to G, g_{\alpha}(x) = x\alpha$$
이 동형사상임을 보이시오. 이 명제는 G가 동질공간 (homogeneous space) 임을 보인다.
풀이.
임의의 $\alpha \in G$에 대해 $f_{\alpha}, g_{\alpha}$가 연속임을 보이면 된다. 이는 $f_{\alpha^{-1}} = f_{\alpha}^{-1}$이기 때문이다.
곱함수 $f: G \times G \to G$를 생각하자. $f_{\alpha}(x) = f(\alpha,x)$임에 주목하라.
이제, G의 열린집합 $\alpha x \in U$를 생각해 보면, $(\alpha,x) \in f^{-1}(U)$이므로, 어떤 기저집합 $V \times W \subset G \times G$가 존재하여 $(\alpha,x) \in V \times W \subset G \times G$가 성립한다.
따라서, $y \in W \Rightarrow f_{\alpha}(y) = f(\alpha,y) \in U$가 성립하여, $f_{\alpha}$는 연속이다. 비슷한 논의를 $g_{\alpha}$에 대해서도 할 수 있다.
5. H가 G의 부분군이라 하자. $x\in G$면, $xH := \{xh| h\in H\}$를 G 내 H의 좌잉여류라 부른다. $G/H$를 H의 좌잉여류들의 집합이라 하자. 이 집합에 몫위상을 부여하자.
(a) $\alpha \in G$면, 4.에서 정의한 함수 $f_{\alpha}$가 $G/H$ 사이의 위상동형사상을 유도하여, $xH$를 $(\alpha x)H$로 보냄을 보이시오. 이 결과는, $G/H$도 동질공간임을 의미한다.
풀이.
몫위상이 뭔지가 가물가물하여 고른 문제이다.
직관적으로 몫위상은 원래 위상공간의 몇몇 점들에 동치류를 부여하여, "같음을 부여하는" 작업이라 할 수 있다.
어떤 함수 $\pi: G \to H$가 전사이고, $G$가 위상공간일 때, f를 "이어붙이는 함수"로 생각한다면, $\pi$를 연속으로 만드는 가장 세밀한 위상을 G에 부여한 것이 몫위상이다.
따라서, $H$의 모든 부분집합의 역상을 생각하여, $S \subset H$에 대해 $f^{-1}(S)$가 $G$에서 열린집합인 경우, 그리고 그 경우에만 $S$를 열린집합으로 선언하는 것이다.
원래 위상공간 G 사이의 사상 $g: G \to G$가 있다 하자. 또한, $g$가 다음 조건을 만족한다 하자:
$$\pi(y) = \pi(y') \Rightarrow \pi(g(y)) = \pi(g(y'))$$
그러면, $h: H \to H$를 다음의 식을 만족하도록 정의하려고 시도해도, 정의가 잘 된다:
$$h\pi = \pi f$$
이제 $f_{\alpha}: G \to G$를 생각해 보자.
$\pi(x) = \pi(y) \Leftrightarrow x^{-1}y \in H$이다.
이제, $(\alpha x)^{-1}(\alpha y) = x^{-1}y \in H$이므로, $\pi \circ f (x) = \pi \circ f(y)$도 만족한다. 따라서 $h: G/H \to G/H$가 잘 정의된다.
$h$가 정의된 방식에 의해, $h_{\alpha}(xH) = f_{\alpha}(x)H = (\alpha x)H$이다.
임의의 $\alpha$에 대해 $h_{\alpha}$가 전단사임은 쉽게 알 수 있으니, 연속함수임을 보이자.
$(\alpha x)H \in G/H, (\alpha x)H \in U$라 하자 (U는 $G/H$서 열린집합).
이제, $xH \in h^{-1}((\alpha x)H)$인데, $xH \in V, h(V) \subset U$를 만족하는 열린집합 V를 잡아야 한다.
$\tilde{U} := f^{-1}\circ \pi^{-1}(U)$는 G에서 열린집합이다. 이제, $\pi(\tilde{U})$가 열린집합이라면, 정의상 문제가 해결될 것이다. 이를 위해 $\pi$가 열린 사상임을 보이자.
보조정리. $\pi$는 열린사상이다.
증명.
$U \subset G$가 열린집합이라 하자. $\pi^{-1}(UH) = \pi^{-1}(\{xH | x\in U\})$가 $G$에서 열린집합임을 보이면 증명이 끝난다. 그런데 $\pi^{-1}(UH) = \{xh | x\in U, h\in H\}$임을 알 수 있다. 이는 다시 $\cup_{h \in H} Uh$인데, 우리가 앞서 살펴보았듯 사상 $g_{h}: G \to G, g_{h}(x) = xh$는 위상동형사상이므로 열린 사상이고, 따라서 이 집합은 열린집합의 합집합이어서 열린집합이다. 따라서 $\pi$는 열린사상이다.
어쩌다가 보니 (c)도 같이 풀었다!
<군과 조화해석>에 나왔던 명제는 다음의 설명으로 갈음한다.
Prop 1.1. (G는 위상군이고, 뒤에 나오는 함수 g는 곱함수이다.)




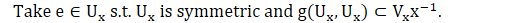






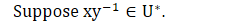



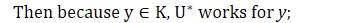

'수학 (2023-S)' 카테고리의 다른 글
| [번외] Geodesic curvature (0) | 2023.08.05 |
|---|